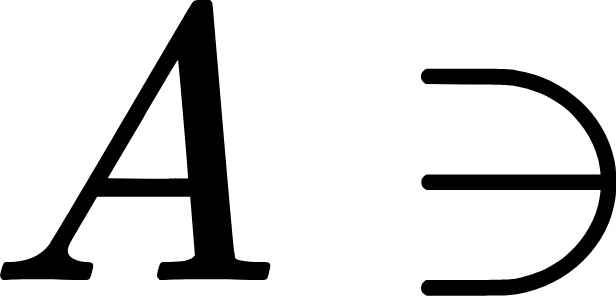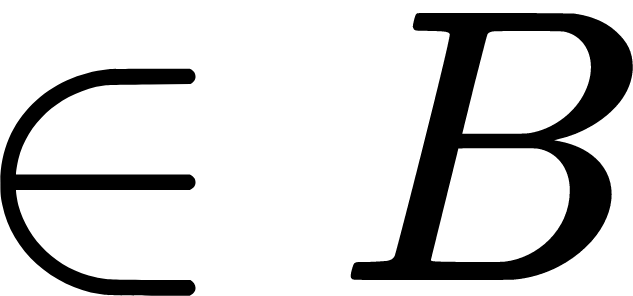Notation for nonempty intersection
There is no standard mathematical symbol for the intersection relation.
You've probably encountered the symbol for the intersection operation. If \(A\) and \(B\) are sets, then "the intersection" of \(A\) and \(B\), denoted \(A \cap B\), is the set of all \(x\) such that \(x \in A\) and \(x \in B\). It's the middle part of a Venn diagram.
That's fine, but I'm talking about the intersection relation. We say that \(A\) "intersects" \(B\) if there exists some \(x\) such that \(x \in A\) and \(x \in B\). To express the condition using symbols, a common approach is to write \(A \cap B \neq \emptyset\). It gets the job done, but it's clunky, it's kind of a double negative, and every time I read it, it's like my mind hits a speed bump.
For comparison, consider the equation \(A \cap B = A\). When I read that equation, I have to do some mental processing before I understand what it is telling me: \(A\) is a subset of \(B\). In contrast, when I see the elegant notation \(A \subseteq B\), the meaning is so clear that I cannot avoid understanding it. (Try reading the word "elephant" and not thinking of an elephant...) I am grateful for the subset symbol. I feel that mathematics would be needlessly hobbled if we were all writing \(A \cap B = A\) instead of \(A \subseteq B\).
I propose that we write \(A \ni\!\in B\) to indicate that \(A\) intersects \(B\). The idea is that the condition \(x \in A \cap B\) can also be written \(A \ni x \in B\). If you erase the \(x\) and smush everything together, you get \(A \ni\!\in B\).
Going forward, I plan to write \(A \ni\!\in B\) in my research papers instead of \(A \cap B \neq \emptyset\). (I'll always include the definition, and if I have coauthors who would rather not use the new symbol, I won't insist.) In TeX, you can typeset the symbol using the commands \ni\joinrel\in. For disjoint sets, you could use the centernot package to get \(A \centernot {\ni\!\in} B\), but I'm not sure it's an improvement over the equation \(A \cap B = \emptyset\).
I'm not the first to suggest notation for intersecting sets. Reddit user nickmcclendon proposed a symbol in 2011. His symbol resembles the amssymb \between symbol, which looks like this: \(A \between B\). I would be fine with that notation or any other reasonable notation. I just want something to catch on and become standard!